I was at SFMOMA with Erika a few weekends ago and we saw an exhibit showing the work of Lebbeus Woods – a futuristic architect and illustrator.

A quote at the beginning of the exhibit caught me off guard… I had never really thought about light this way:

I dearly love the form of things. Particularly because forms make light visible, and light is a sublime substance. We only see light when it is reflected from the surfaces of forms and the diverse materials of which they are made. It is not only that light pervades the universe and is a kind of messenger of the histories and mysteries of time and space....
- Lebbeus Woods

This thought stuck with me: the whole history of Earth and Mankind is still out there in the universe, streaming away in an expanding sphere of light.

What if we could get out there somewhere and see that light? It would be like time travel with read-only access.

As I walked around the rest of the exhibit I started to get a crazy thought…

6,000 years ago, our ancestors were wandering around the globe with pointy little spears. And, just like every day since, the Sun was shining and light was reflecting off their heads, back into space.

Over the next 3,000 years that light zipped off into the galaxy, never to be seen again.

But suppose a tiny portion of that light was headed right for a black hole.

And then suppose a tiny portion of that tiny portion of light encountered the black hole at just the right angle so that it wasn’t sucked away forever. But instead, got bent exactly 180 degrees, boomeranged around the black hole and headed straight back to Earth.

After the second 3,000 year leg of its journey, that light is streaming back through your window.

The idea is tantalizing to me – that by staring at a black hole we could literally look back in time. I couldn’t put it to rest, so I dug through some physics literature and pieced together just how (in)feasible this observation would be.

It turns out it’s possible. Almost.

Gravitational Lensing

According to Einstein’s Theory of General Relativity, light is affected by massive objects because they curve spacetime. We don’t need to understand the physics deeply. The point is that massive objects like black holes and galaxies can bend light significantly:

This is picture a of Einstein’s Cross, a distant “Quasar” repeated four times, gravitationally lensed around the galaxy in between us and the Quasar.

But just how far does the light bend? For low deflection angles the calculation is straight forward, but we’re interested in light that’s practically grazing the surface of the black hole. These higher deflection angles are extremely complicated to calculate, but Valerio Bozza put it together in 2007:

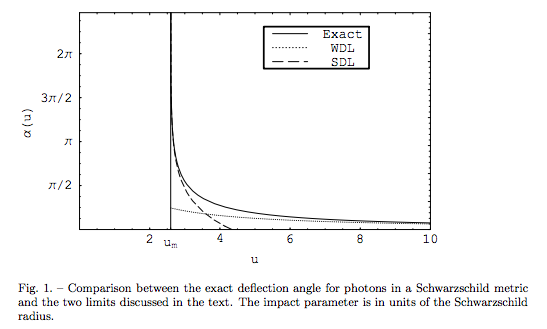
Below the asymptote on that plot is where light gets sucked into the black hole and is never seen again. But we don’t want that, we want the light to be completely reflected.

To be reflected, so that we could see ancient Earth in the black hole, we’d need a deflection of 180 degrees, or pi radians. Looking at the graph you can see that this “reflection” happens near the asymptotic “edge” of the black hole.

But then there’s noise.

The biggest black holes sit at the center of galaxies and have masses millions of times bigger than our Sun.

These seem like perfect candidates for observing our “reflection” but there’s a glaring problem. Around these huge black holes there’s an accretion disk of gas, with stars colliding and exploding everywhere. This creates a huge amount of light that would drown out any “reflection” of ancient Earth.

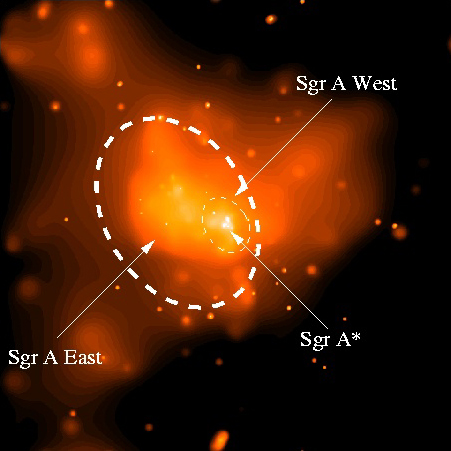
If you take a look at Sagittarius A*, the black hole at the center of our own galaxy, you’ll see what I mean. We could never spot ourselves in the middle of this:

What we need is a nice, simple black hole that’s minding it’s own business in a quiet neighborhood.

We’re looking for a MACHO.

MACHO is a whimsical name for “dark” massive objects. It includes black holes that don’t have big messy accretion disks.

The only way we can detect a MACHO is when it moves between us and a distant galaxy, creating a “gravitational lensing event” where the brightness of the distant object suddenly increases and decreases:

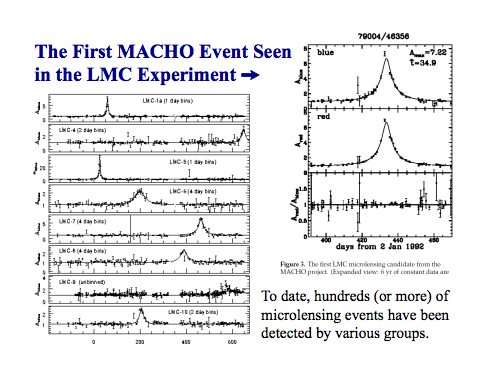
These MACHOs are much better candidates for our attempt to observe a “reflection” of the Earth or our Sun. The best candidate so far is a black hole named MACHO-96-BLG-5, which was observed at a distance of about 3,000 light years from Earth. It’s “best” because it’s the closest one we’ve ever seen, and closer means the “reflection” of ancient Earth would be brighter.

Could we see ourselves in MACHO-96-BLG-5?

In 2002 Daniel Holz and John Wheeler investigated this idea and ran all the calculations in their paper Retro-MACHOs: Pi in the Sky?

The short answer is no, not with current telescopes.

The problem is that even the “reflection” of the Sun is far too dim. Holz and Wheeler ran the calculations for hypothetical black holes that might wander within a couple light-years of Earth. Under those unlikely circumstances, observing the reflection is doable with existing telescopes, or on the brink of doable with telescopes being planned.

Here’s their results for black holes (BH) with 1 or 10 times the mass of the sun, within 1 parsec (3.24 light-years) of Earth:

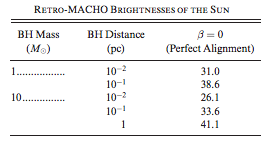
To help you understand the magnitude scale: a higher positive magnitude is dimmer. The Sun at noon is magnitude -27. The full Moon is -13. The Hubble Space Telescope has detected stars with a magnitude of just 30. As you can see in the table, Hubble might just barely be able to observe the reflection in some (improbable) cases.

Their results are for MACHOs we might observe, but for MACHO-96-BLG-5 they simply say there’s no way we could observe the Sun in the “reflection”… which means the magnitude must be 50 or higher. Extremely dim.

So we need a better telescope.

The light-gathering capacity of a telescope is limited by the surface area of its mirrors. The Hubble has a collecting area of 4.5 square meters and a diameter of 2.4 meters.

In order to observe a magnitude 40 observation like the one in the table above, we’d need a 240 meter diameter telescope. For a magnitude 50 observation, we’d need a 24 kilometer diameter telescope. The largest telescopes currently under consideration are the European Extremely Large Telescope or the even more hilarious Overwhelmingly Large Telescope with diameters of 40 meters and 100 meters each.

So even though occasional photons from 6,000 year-old ancient Earth are coming back through your window, it’ll be a while before we can see them.

Maybe there’s a better MACHO?

The hunt for more MACHOs is still on. And there’s good hope that we’ll find one significantly closer than 96-BLG-5.

According to research published in 2002 the expected density of MACHO black holes in the vicinity of the Sun suggests that there’s probably a MACHO within 10 parsecs (32.4 light-years) of Earth. Of course, then you’d only be looking back at an “ancient Earth” from 65 years ago.

Until then, let’s figure out how to build bigger space telescopes :)