Crossing the United States on a train is an incredible experience. North Dakota fields ooze an evil early-morning fog that will make your spine shiver. The Montana Rockies tower suddenly from the endless plains. When you slip by at 40,000 ft in an aluminum tube you are missing this magic.

So why not take the train? Because it takes 3 days @ $208 one-way to get from Boston’s South Station to Seattle’s King St. Station, a trip of about 3,000 miles. I would take the train every time if it took less than a day and still didn’t cost a fortune.

So less than a day would be cool, but…. just how fast could you cross the country (without killing yourself)? The question is NOT about technological limitations, those change every day. The question is really about the “without killing yourself” part.

Magical Tech

For the technology, let’s assume something like a vacuum tube with a maglev train, unrestricted by air resistance and without physical contact points to a physical track. The hypothetical train’s deceleration could transfer energy back out, so the whole system would be extremely energy efficient…. low variable costs per trip but extremely high fixed costs to build the system.

Without Killing Yourself

What about physiological limitations? Martin Voshell has put together a fascinating history of US Colonel Stapp’s experiments on acceleration and the human body (section 2.1). In 1954 Colonel Stapp survived 46.2 g’s, decelerating “eyeballs out” from 632 mph to 0 mph in 1.4 seconds. This a bit extreme for civilian transport, especially since this was a momentary peak and not sustained. A 1960 technical note from NASA explains that pilots in centrifuges tolerated accelerations of 17 g’s “eyeballs in” and 12 g’s “eyeballs out”. According to NASA the Space Shuttle has a maximum acceleration was 3 g’s, which Wikipedia claims is “largely for astronaut comfort.”

Given that “eyeballs in” (accelerating while facing forward) is more tolerable, let’s work with those numbers. Assume that the seats on our futuristic maglev vacuum-tube train can rotate 180 degrees so that deceleration is also “eyeballs in.” Reasonable accelerations seem to be 3 g’s for comfort, or 17 g’s for “tolerable”/”not dead, yet… just a fleshwound!”

Start Your Calculators

Let’s assume our maglev can sustain maximum acceleration halfway across the country, then decelerate the other half, which is as fast as you can go. Here’s a plot of cross-country travel time vs. sustained acceleration.

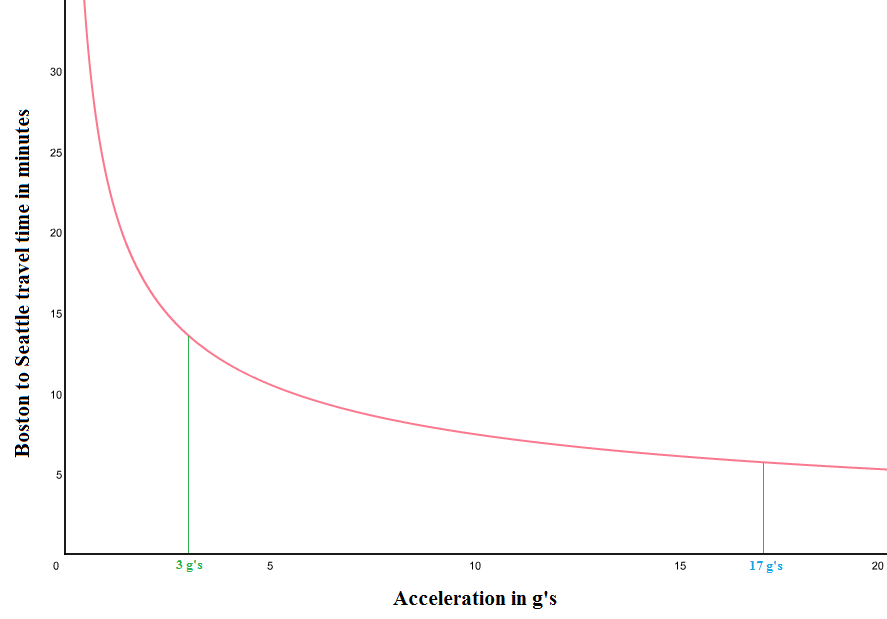
Constantly accelerating/decelerating at 3 g’s will get you from Boston to Seattle in just under 15 minutes. If instead you want to be crushed into your seat and blacked out at 17 g’s, you can get to Seattle in about 7 minutes. North Dakota would blow by in about 16 seconds… probably defeating the whole eerie fog experience. You can find the original plot & equation in metric units here (good work desmos, though an embeddable version and the ability to label the axes and annotate the plot would be awesome!)

Another interesting by-product of accelerating continuously halfway to your destination is that the time required to get to the destination scales with the square root of the distance…. so travel times don’t vary as much as you would expect. This table shows one-way travel times for a 3 g acceleration:

Beijing: 20 minutes to cross 11,000 km
Seattle: 12 minutes to cross 4,000 km
Chicago: 7 minutes to cross 1,400 km
New York: 3 minutes to cross 360 km

You can find the original plot and equation in metric units here (time in minutes vs. distance in kilometers).

As far as human limitations go, rail transit clearly has a lot of room for improvement. A ~350x reduction in travel time for cross-country rail trips is possible, purely from a physiological perspective :)

For a much more thorough, and brutally honest analysis of urban transportation: http://swiftprt.com/blog/2011/12/the-future-of-ground-based-transportation-systems/